What is the Dozenal System?
The Dozenal System is a way of counting, computing, and all around using numbers in a base-12 system. 'Dozenal' comes from the word 'Dozen', thus the digits would be in a set of twelve rather than the conventional ten.
The digits that are used are as follows:
X is pronounced as 'Dek', and E is pronounced as 'El'.
When learning this system, simple arithmetic is the place to start:
9 + 1 = XX + 1 = EE + 1 = 10This last one is true because we have run out of digits and must then carry over, just like we do in the decimal system (Base 10).
One argument against the dozenal system is that humans have 10 fingers, and that's why we use base 10. But rest assured that we do use base 12 in various places. In the imperial system we have 12 inches in a foot. There are 2 sets of 12 hours in every day. There are 12 months in a year. And eggs usually will come in a dozen.
As for fingers, try counting with your thumb this way:
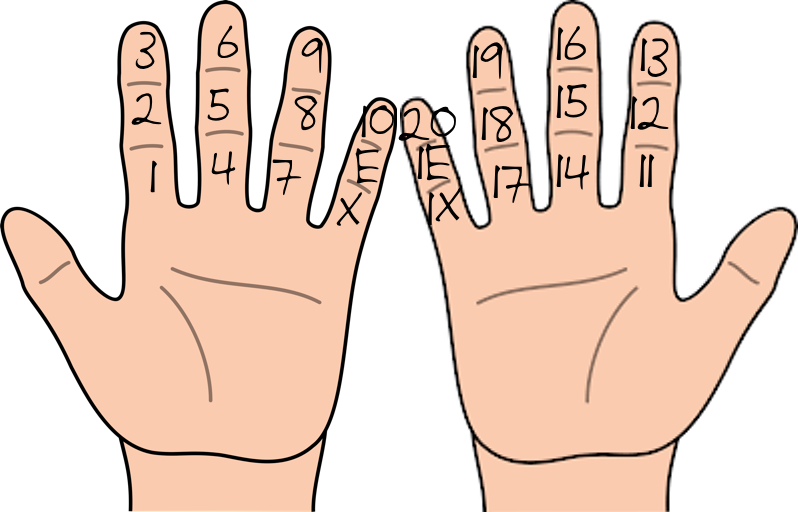
Thus you can count to dozenal 10 on one hand.
The main argument for using this system is the number of factors found in a dozenal system. In this system, dozenal 10 (now equivalent to decimal 12) would be divisible evenly by 2, 3, 4, and even 6. Decimal 10 is only divisible by 2 and 5. I mean, how often do you need to split things 2, 3, or 4 ways? Probably WAY more often than 5 ways, right?
All mathematics would still work, regardless of base (as computers do just fine with Binary), but from an aesthetically pleasing methodology, it would be generally easier for the average person to converse in dozenal, rather than decimal, given that they were taught evenly in both.
For a practical application in this system, check out my time-keeping article.
Or if you want to test your mathematical prowess in the dozenal system, be sure to try your hand at this addictive Bubble Popping game.